Utilizziamo come esempio il dataset di esempio cars incluso nel pacchetto datasets, e che raccoglie i dati relativi a velocità (speed) e spazio di frenata (dist) di 50 automobili.

# carichiamo i pacchetti
library(tidyverse)

Il modello di regressione utilizza la funzione della retta per rappresentare la forma della relazione fra due variabili. Più la relazione è lineare (direttamente o indirettamente proporzionale), più i valori di Y potranno essere calcolati (predetti) in base a quelli di X, grazie alla funzione della retta:

$$Y = a + bX + e$$

dove:

• $b$ = coefficiente di regressione, e indica l’inclinazione della retta (coefficiente angolare);
• $a$ = intercetta della retta sull'asse delle ascisse;
• $e$ = errore, ovvero la distanza fra valori attesi e valori reali.

In ipotesi, i valori osservati di $Y$ dovrebbero crescere (o diminuire) in media di una proporzione fissa pari a $b$, a meno di un errore $e$ ¹⁾.

L’equazione di un modello di regressione lineare può essere scritta anche come:

$$\hat Y = \beta_0 + \beta_1 X$$

Dove i parametri $\beta_0$ e $\beta_1$ sono i coefficienti del modello, rispettivamente l’intercetta e la pendenza della retta di regressione, e dove $\beta_1$ viene chiamato regressore (o anche predittore), e “peso” della variabile $X$.

Questa notazione è utilizzata in particolare nei modelli lineari generalizzati e nel campo del machine learning²⁾.

Obiettivo del modello è calcolare i coefficienti $a$ e $b$, minimizzando l’errore (o perdita, o loss), ovvero valori attesi di $Y$ ($\hat Y$), dati i valori osservati di $X$, che si discostano il meno possibile dai valori osservati di $Y$.

$$\hat Y = a + bX$$

Nel linguaggio di R (vedi: formula) scriveremo:

$$Y \sim X$$

Gli assunti del modello sono:

• la linearità della relazione;
• l'indipendenza dei residui;
• l'omoschedasticità (varianza costante) dei residui;
• normalità della distribuzione dei residui, con media pari a zero.

Per quanto riguarda la linearità della relazione, possiamo valutare a priori, attraverso un grafico di dispersione o Scatterplot (grafico a dispersione) se la relazione fra le due variabili abbia un andamento almeno grosso modo lineare: .

Ipotizziamo che lo spazio di frenata aumenti con la velocità: $Y=f(X)$, quindi X (indipendente) = speed e Y (dipendente) = dist

Eseguiamo le seguenti righe di comando:

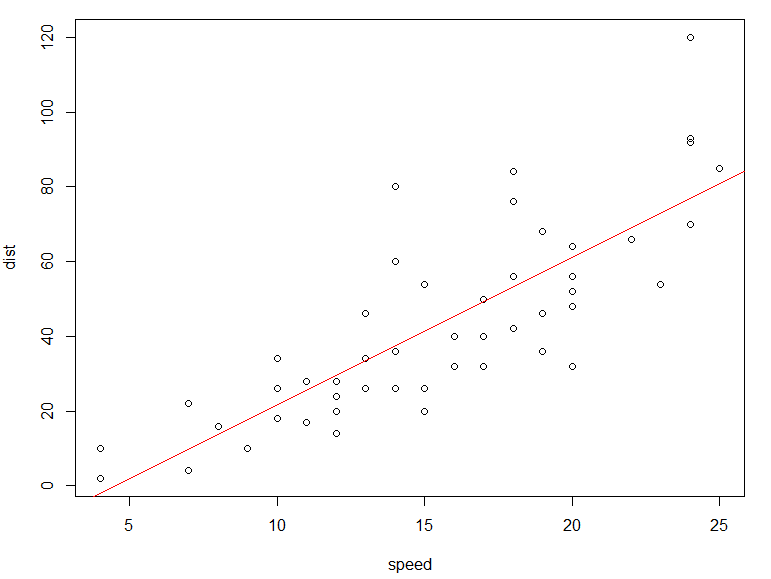
# costruisco il grafico delle due variabili
# prima la variabile X, poi la variabile Y
plot(cars$speed, cars$dist, ylab = "dist", xlab="speed")
 
# aggiungo la retta dei minimi quadrati
abline(lm(cars$dist ~ cars$speed), col = "red")

con ggplot (vedi I grafici con ggplot2)

ggplot(cars, aes(speed, dist)) +    # sistema di riferimento
  geom_point() +                    # punti
  geom_smooth(method = "lm")        # geom_smooth: interpolazione

Il grafico prodotto conferma la plausibilità dell'assunto di linearità: lo spazio di frenata aumenta in maniera uniforme all'aumentare della velocità.

Osserviamo però anche che i punti non sono perfettamente allineati e si discostano dalla retta.

L’errore da minimizzare è un problema di non univoca definizione e soluzione, in quanto può essere calcolato in diversi modi, anche per lo stesso modello. Ci riferiamo a questi diversi modi con l’espressione funzione di perdita (loss function). Nel modello di regressione lineare semplice il valore che viene minimizzato è la somma dei quadrati delle distanze fra i valori osservati e quelli previsti dal modello (metodo dei minimi quadrati).

Passando dalla media di $Y$, alle medie “locali” (i punti blu), alla retta dei minimi quadrati, abbiamo guadagnato in sintesi ed interpretabilità della relazione, nonché di capacità previsionale, e abbiamo perso qualcosa in termini di variabilità spiegata di $Y$, che non sarà più pari a 1, a meno che i punti non siano perfettamente allineati lungo la retta di regressione.

La funzione utilizzata per lo studio dei modelli lineari è lm(), il cui argomento principale è la formula che rappresenta il modello da utilizzare, nella forma lm(dist ~ speed).

Eseguiamo dunque le seguenti righe di comando:

res <- lm(dist ~ speed, data=cars)

summary(res) 

## 
## Call:
## lm(formula = dist ~ speed, data = cars)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -29.069  -9.525  -2.272   9.215  43.201 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -17.5791     6.7584  -2.601   0.0123 *  
## speed         3.9324     0.4155   9.464 1.49e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 15.38 on 48 degrees of freedom
## Multiple R-squared:  0.6511, Adjusted R-squared:  0.6438 
## F-statistic: 89.57 on 1 and 48 DF,  p-value: 1.49e-12

Analizziamo i risultati. In primo luogo, troveremo il comando che ha definito il modello stesso:

##  Call:
##  lm(formula = dist ~ speed, data = cars)

Seguono le statistiche descrittive della distribuzione dei residui, ovvero delle differenze fra valori osservati e valori attesi sulla base del modello:

##  Residuals:
##      Min      1Q  Median      3Q     Max 
##  -29.069  -9.525  -2.272   9.215  43.201 

Poiché infatti la normalità dei residui è uno degli assunti del modello, i valori della loro distribuzione ci vengono proposti per primi. In questo caso, i risultati indicano che i residui sono solo leggermente asimmetrici, come si nota dalla differenza interquartile e dal valore della mediana (la media dei residui è pari a 0).

Per controllare la normalità dei residui possiamo usare un test di normalità, ad esempio applicando la funzione shapiro.test() al risultato della funzione residuals():

shapiro.test(residuals(res))

## 
##  Shapiro-Wilk normality test
## 
## data:  residuals(res)
## W = 0.94509, p-value = 0.02152

L'errore standard dei residui è una misura della dispersione dei residui attorno alla retta di regressione. Si calcola con $\sqrt{\text{residui}^2/df}$

sqrt(sum(res$residuals^2)/48)
##  [1] 15.37959

Possiamo ottenere questo valore con la funzione

sigma(res)
##  [1] 15.37959

##  Residual standard error: 15.38 on 48 degrees of freedom

Passiamo a questo punto a considerare i parametri del modello, ovvero i coefficienti a (intercetta, intercept) e b (indicato con il nome della variabile esplicativa, speed) della retta di regressione:

##  Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
##  (Intercept) -17.5791     6.7584  -2.601   0.0123 *  
##  speed         3.9324     0.4155   9.464 1.49e-12 ***
##  ---
##  Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Per ciascun parametro della retta, vengono forniti: il valore stimato (Estimate), l’errore standard (Std. Error), il valore t (t value), e il valore Pr(>|t|) che è il valore di probabilità del test t a due code.

L’intercetta (-17,58) indica lo spazio di frenata quando la velocità è pari a 0, ovvero quando l’auto è ferma: valore che naturalmente non ha alcun senso in questi termini, ma che dipende essenzialmente dalle relative scale e non ha un significato sostantivo.

Il parametro che interessa è però il coefficiente di regressione è pari a 3,9324, e ci informa sulla forma della retta che interpola i punti, ma nulla sulla forza della relazione in quanto tale.

Se le due variabili covariassero in maniera lineare, la retta avrebbe questa forma.

Per calcolare gli intervalli di confidenza dei parametri del modello (di questo e di altri), possiamo utilizzare la funzione confint():

confint(res)
 
##                  2.5 %    97.5 %
## (Intercept) -31.167850 -3.990340
## speed         3.096964  4.767853

Ma è il coefficiente di determinazione R² la misura della qualità della stima prodotta dal modello, in termini di varianza spiegata: Nel nostro caso, quindi, R² è pari a 0,65, a dire che la varianza di Y (dist) spiegata dal modello lineare è pari al 65% della sua varianza complessiva; con i tre outliers in meno, il valore di R² sale a 0,72.

##  Multiple R-squared:  0.6511,	Adjusted R-squared:  0.6438 
##  F-statistic: 89.57 on 1 and 48 DF,  p-value: 1.49e-12 

L'output include anche il valore dell’R² corretto, usato nella regressione multivariata.

Per valutare la significatività statistica di R², si utilizza invece il test F: il numero di gradi di libertà del modello è pari al numero dei coefficienti (in caso di regressione bivariata, 1); il numero dei gradi di libertà della distribuzione congiunta delle due variabili è pari al numero dei casi, meno il numero dei parametri (48).

Passiamo ai grafici standard del risultato di lm(), che di fatto si concentrano anch’essi sui residui

plot(res)

I grafici verranno prodotti in sequenza:

  > plot(lm.res)
  Premi <Invio> per vedere il prossimo grafico: 

I grafici mostrano:

• Residuals vs Fitted: La linea orizzontale rappresenta la media dei residui, pari a 0 per definizione. La linea rossa è una curva di smoothing non parametrica (LOESS), che serve a visualizzare la tendenza media dei residui al variare dei valori predetti: se la relazione fosse lineare e gli errori fossero omoschedastici, la linea rossa coinciderebbe con quella della media (cioè a 0). I residui sono distribuiti casualmente attorno a 0, ma si evidenziano degli outliers.
• Q-Q plot: mostra la normalità di una distribuzione (in questo caso, dei residui): anche qui si evidenziano degli outliers sui valori alti (vedi: Grafici quantili-quantili).
• Scale-Location: mostra la distribuzione dei residui standardizzati in funzione dei valori previsti dal modello. Serve in particolare a verificare l’assunzione di omoschedasticità (varianza costante degli errori): se la linea rossa è approssimativamente orizzontale, suggerisce che la varianza dei residui è costante.
• Leverage: Questo grafico aiuta a identificare le osservazioni che hanno un’influenza (leverage) maggiore sui risultati del modello, cioè i punti che hanno un impatto sproporzionato sulla stima dei coefficienti del modello (gli outlier). In questo caso, la linea rossa può aiutare a vedere se i punti più influenti tendono ad avere residui più grandi o più piccoli, per identificarli.

Per produrre uno solo di questi grafici, ad esempio il Q-Q plot:

plot(res, which = 2)

Le funzioni fitted() e predict() restituiscono dunque i valori attesi in base al modello:

$$\hat {\text{speed}} = -17,58+3,9 \text{dist}$$

-17.5791 + (3.9324 * cars$speed)

restituisce — a meno di approssimazioni — gli stessi valori di

fitted(res)

e di

predict(res)

La funzione predict() può però essere applicata ad un diverso dataset — appunto in funzione predittiva.

Ad esempio, costruiamo un dataframe che contenga (almeno) la variabile indipendente (speed):

new.data <- data.frame("speed"=c(5, 50, 23, 12))

predict(res, newdata = new.data)

Valori previsti per la variabile dist, in base ai dati del modello (training data):

##         1          2          3          4 
##  2.082949 179.041343  72.866307  29.609810

Vedi: Funzioni per esplorare i modelli

La scomposizione della devianza è utile per comprendere la quantità di variabilità spiegata dal modello rispetto alla variabilità totale, ma soprattutto per confrontare modelli diversi, con più regressori, e valutare la significatività del contributo che ciascuno porta alla spiegazione della variabilità di $Y$.

Vedi Modelli lineari e scomposizione della devianza

Vedi Regressione lineare: Individuare gli outliers e ripetere l'analisi

In caso di regressione bivariata, il coefficiente di regressione può essere calcolato come rapporto fra covarianza e varianza della variabile assunta come indipendente:

$$b_{yx} = \frac{covXY}{varX} = \frac{\sigma_{xy}}{\sigma^2_x}$$

$$b_{xy} = \frac{covXY}{varY} = \frac{\sigma_{xy}}{\sigma^2_y}$$

cov(cars$speed, cars$dist) / var(cars$speed)
##  [1] 3.932409
 
cov(cars$speed, cars$dist) / var(cars$dist)
##  [1] 0.1655676

Il prodotto dei due coefficienti di regressione è uguale al coefficiente di determinazione $R^2$:

$$b_{yx} b_{xy} = R^2 = \frac{\text {devianza spiegata}}{\text {devianza totale}}$$

3.932409 * 0.1655676
##  [1] 0.6510795

La radice quadrata di $R^2$, e dunque del prodotto dei due coefficienti di regressione è il coefficiente di correlazione $r$.

$$ r = \sqrt{b_{yx} b_{xy}} $$

sqrt(3.932409 * 0.1655676)
##  [1] 0.806895

Considerando le relazioni fra queste grandezze, in caso di relazione bivariata, e una volta controllati gli assunti della correlazione, è sufficiente in fase esplorativa svolgere il test di correlazione (per avere una misura di significatività), e valutare l’adeguatezza del modello.

E' possibile scaricare ed eseguire lo script dell'esempio:

Es-lm-bivariata.R

# grafico della retta dei minimi quadrati
plot(cars$speed, cars$dist, ylab = "dist", xlab="speed")
abline(lm(dist ~ speed), col = "red")
 
# con ggplot2
library(ggplot2)
 
ggplot(cars, aes(speed, dist)) +
  geom_point() +
  geom_smooth(method = "lm")
 
# lm  
res <- lm(dist ~ speed, data = cars)
summary(res)
 
# intervalli di confidenza
confint(res)
 
# errore standard dei residui
sigma(res)
 
# regressione e correlazione
cov(cars$speed, cars$dist) / var(cars$speed)
cov(cars$speed, cars$dist) / var(cars$dist)
3.932409 * 0.1655676
sqrt(3.932409 * 0.1655676)