Nei modelli di regressione lineare, alcuni casi, noti come “outliers”, possono avere un impatto sproporzionato sui risultati, in quanto esercitano un'influenza eccessiva sulla stima della retta di regressione.

Si tratta di osservazioni i cui valori osservati sono particolarmente distanti da quelli previsti dal modello, che possono essere identicati utilizzando i grafici diagnostici, e metriche specifiche quali i residui standardizzati (che evidenziano i valori lontani dalle previsioni) e la distanza di Cook (che misura l'influenza di un singolo punto sul modello).

Una volta individuati gli outliers, si ripete l'analisi escludendoli per valutare come cambia l'adattamento del modello, osservando ad esempio un miglioramento del coefficiente $R^2$.

Escludere gli outliers non è però sufficiente: in particolare, è fondamentale capire se si tratta di semplici errori di misurazione da espungere, o se rappresentano casi particolari e significativi che non dovrebbero essere ignorati.

Partiamo considerando l'esempio della pagina dedicata alla regressione lineare semplice.

library(tidyverse)

Costruiamo il modello

res <- lm(dist ~ speed, data=cars)

E guardiamo i grafici previsti dalla funzione lm() (per i comandi, ì vedi qui)

plot(res)

In tutti e quattro i grafici in Fig. 1, vengono evidenziati degli outliers (con il numero di riga):

• In base ai residui, nei grafici:
  • Residuals vs Fitted: se la relazione fosse lineare e gli errori fossero omoschedastici, la linea rossa coinciderebbe con quella della media (cioè a 0). I residui sono distribuiti casualmente attorno a 0, ma si evidenziano degli outliers.
  • Q-Q plot, che controlla la normalità della distribuzione dei residui (vedi: Grafici quantili-quantili)
• In base ai residui standardizzati, nel grafico: Scale-Location;
• In base alla distanza di Cook e ai residui standardizzati, nel grafico Leverage, che vedremo meglio nel seguito.

Per individuarli nel nostro dataset, usiamo le funzioni per esplorare i modelli, e quelle del pacchetto Broom.

I residui standardizzati misurano essenzialmente di quante deviazioni standard un'osservazione si discosta dal valore previsto dal modello di regressione.

Se gli assunti del modello di regressione sono rispettati (in particolare, la normalità degli errori), ci aspettiamo che questi residui standardizzati si distribuiscano approssimativamente come una distribuzione normale standard.

Di conseguenza, un residuo standardizzato con un valore assoluto superiore a 2 si trova al di fuori dell'intervallo in cui ci aspettiamo che ricada il 95% delle osservazioni.

Di conseguenza, abs(rstandard(res)) > 2 è un modo comune per identificare gli outliers.

La funzione rstandard() estrae il vettore dei residui standard del modello:

st_resid <- rstandard(res)

Con la funzione (base) which() individuiamo i casi in cui il valore supera 2 in valore assoluto (abs()):

# vettori degli indici degli outliers
index <- which(abs(st_resid) > 2)
index

  ##  23 35 49 
  ##  23 35 49 

Abbiamo individuato i casi evidenziati in tutti i grafici visti sopra, escluso quello che fa ricorso anche alla distanza di Cook.

Infine, per espungerli dal dataset originario:

cars[-index,]

La distanza di Cook (Cook's distance) è una misura di influenza (leverage), che indica quanto cambierebbe l'intero modello di regressione se un singolo punto venisse rimosso. Un'alta distanza di Cook significa che quel punto sta “tirando” la retta di regressione verso di sé.

Per calcolare questa misura, usiamo la funzione cooks.distance()

cooks_d <- cooks.distance(lm.res)

Le soglie comunemente accettate sono due:

1. Distanza > 1: Questa è considerata una soglia critica. Un punto con una distanza di Cook superiore a 1 è quasi universalmente considerato un outlier molto influente che probabilmente distorce il modello.
2. Distanza > 4/n: Questa è una soglia di attenzione, molto più comune e sensibile. Qui, $n$ è il numero di osservazioni nel tuo dataset (es. nrow(cars)). Un punto che supera questa soglia ha un'influenza superiore alla media ed è da valutare.

index_2 <- which(cooks_d > 4 / nrow(cars))
 
index_2

  ## 23 49 
  ## 23 49 

In questo caso, gli outliers individuati sono due e non tre, in quanto R evidenzia (almeno) i tre casi con i valori più alti.

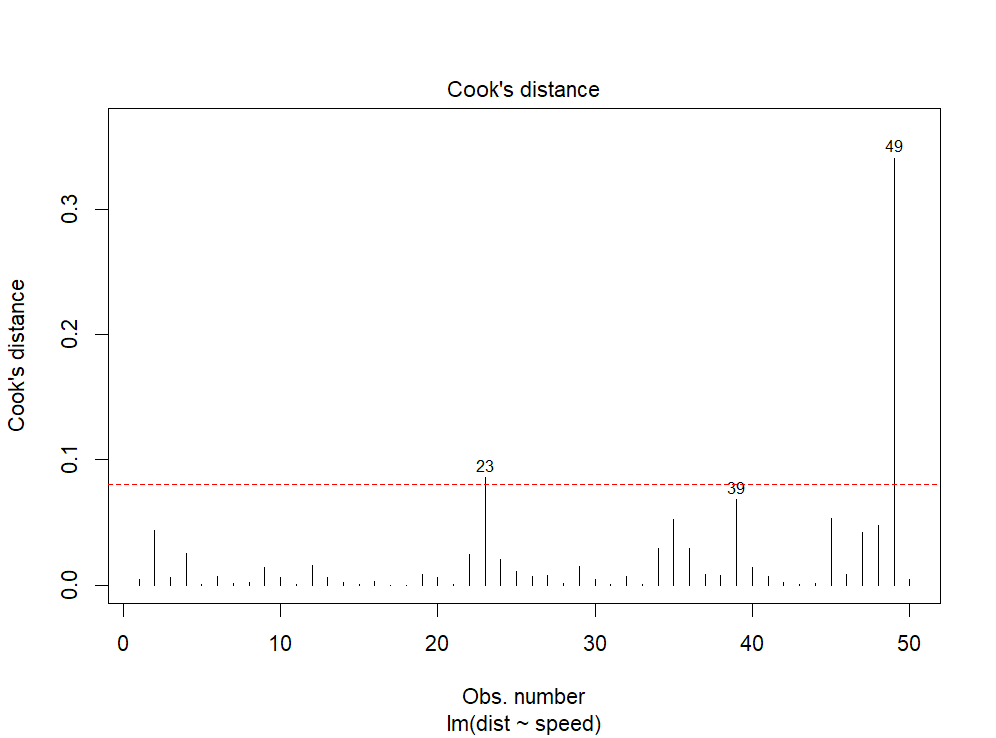
Infatti, se confrontiamo la soglia 4/nrow(cars), possiamo osservare che il caso 39 è al di sotto:

plot(res, which = 4)
abline(h = 4/nrow(cars), col = "red", lty = 2)

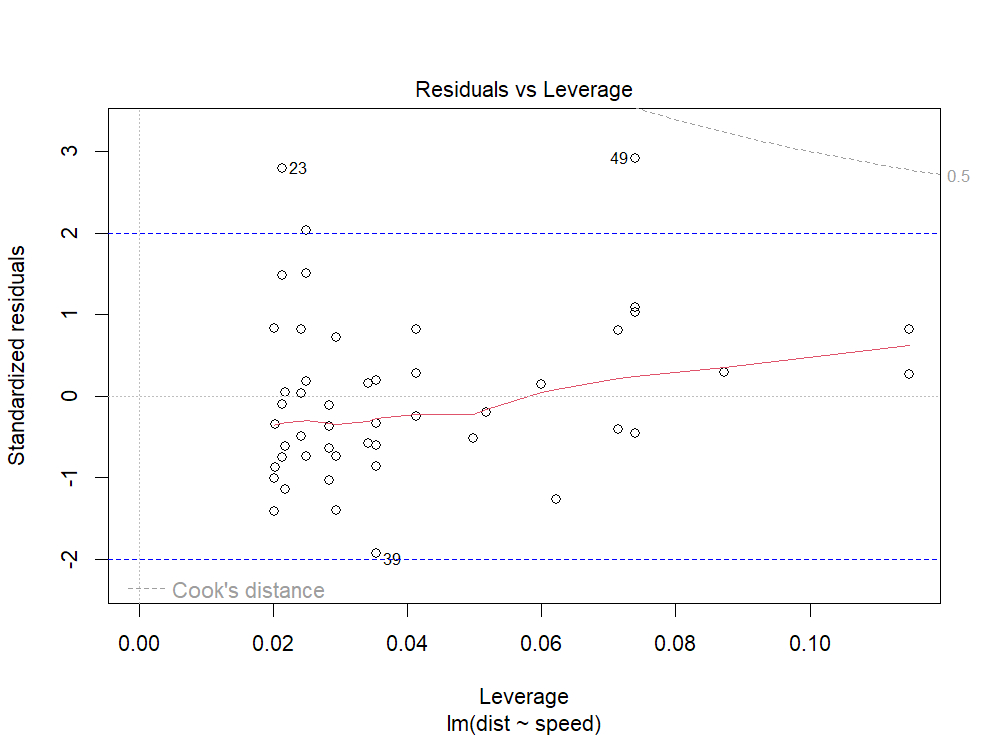
Se confrontiamo la distanza di Cook con i residui standardizzati, il caso 39 rientra nell'area ±2 (altrimenti sarebbe uscito anche utilizzando i residui standardizzati.

plot(res, which = 5)
abline(h = c(-2, 2), col = "blue", lty = 2)

Se considerarlo o meno fra gli outliers, è decisione dell'analista. Per questo, è importante imparare a interpretare i grafici diagnostici, e ad usare le misure diagnostiche fornite sia da R base, che dal pacchetto *Broom*.

E ripetiamo l'analisi, escludendoli:

# modello senza outliers
lm2.res <- lm(data=cars[-c(23, 35, 49),], 
              dist ~ speed)

summary(lm2.res)

## 
## Call:
## lm(formula = dist ~ speed, data = cars[-c(23, 35, 49), ])
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -25.032  -7.686  -1.032   6.576  26.185 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -15.1371     5.3053  -2.853  0.00652 ** 
## speed         3.6085     0.3302  10.928    3e-14 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 11.84 on 45 degrees of freedom
## Multiple R-squared:  0.7263, Adjusted R-squared:  0.7202 
## F-statistic: 119.4 on 1 and 45 DF,  p-value: 3.003e-14

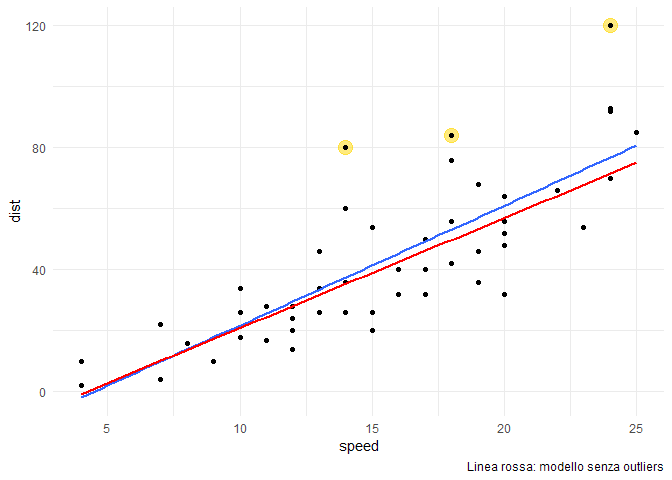
La devianza spiegata dal modello senza outliers è aumentata, e il coefficiente di determinazione $R^2$ è salito a 0,73.

Detto ciò, resta la necessità di comprendere le ragioni di questi outliers: se sono errori di misura non recuperabili, è corretto espungerli dall’analisi; ma potrebbero anche essere casi particolari che non possiamo ignorare … volendo mantenere un certo grado di sicurezza delle strade.

E' possibile scaricare ed eseguire lo script dell'esempio:

nome_file.R