Indice
La correlazione lineare
Il coefficiente di correlazione lineare di Pearson misura l’associazione fra due variabili numeriche, sulla base del confronto fra le varianze. È il rapporto fra la covarianza di due variabili, e il prodotto dei loro scarti quadratici medi1).
$$\frac{S_{XY}}{S_X S_Y}$$
Il coefficiente di correlazione varia da −1 a +1, indicando la direzione (diretta o inversa) della relazione stessa. È però simmetrico, nel senso che non tiene conto della differenza fra variabile indipendente e variabile dipendente.
L'uso di questa misura presuppone che le variabili siano estratte da campione casuale ed abbiano un’andamento normale, e che la loro relazione si approssimi alla linearità, e cioè che, al variare di X, Y vari corrispondentemente in maniera costante e regolare.
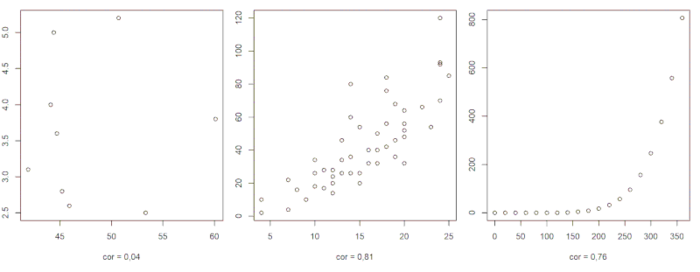
Nel terzo grafico, ad esempio, il coefficiente di correlazione sottostima la relazione fra le due variabili (i punti sono perfettamente allineati, ma non formano una retta).
La funzione ''cor()''
Per calcolare il coefficiente di correlazione, usiamo la funzione cor():
data(cars) cor(cars$speed, cars$dist) ## [1] 0.8068949
Le due variabili condividono l’80,7% della varianza.
Sempre con la funzione cor(), possiamo visualizzare la matrice di correlazione delle variabili di un dataset (sempre che, naturalmente, questo sia composto da sole variabili numeriche):
cor(cars) ## speed dist ## speed 1.0000000 0.8068949 ## dist 0.8068949 1.0000000
A seconda del metodo selezionato, verrà calcolato l'indice di correlazione di Pearson, il tau di Kendall o l'il rho di Spearman
Di default, non esclude i casi mancanti. Per escluderli, usare il parametro na.rm = TRUE
Non calcola la significatività statistica dell'indice. A questo scopo, bisogna usare cor.test.
La funzione ''cor.test()''
Per valutare la significatività statistica del coefficiente di correlazione, e il relativo intervallo di confidenza, possiamo utilizzare la funzione cor.test(), che effettua un test t.
L'ipotesi nulla è che il valore di r sia uguale a 0, quella alternativa è che il coefficiente sia significativamente diverso da 0 (test a due code).
cor.test(cars$speed, cars$dist) ## Pearson's product-moment correlation ## ## data: cars$speed and cars$dist ## t = 9.464, df = 48, p-value = 1.49e-12 ## alternative hypothesis: true correlation is not equal to 0 ## 95 percent confidence interval: ## 0.6816422 0.8862036 ## sample estimates: ## cor ## 0.8068949
Il numero dei gradi di libertà è n − 2 (si sottraggono le due medie al numero dei casi); l’ipotesi nulla può essere respinta (p = 0). L'intervallo di confidenza del 95% ha come estremi 0,68 e 0,89, ad indicare la “forbice” del valore nella popolazione da cui è stato estratto il campione.
Parametri e uso
| x,y | vettori numerici di uguale lunghezza |
| alternative | ipotesi alternativa all'ipotesi nulla |
| method | “pearson”, “kendall”, “spearman” |
| exact | usato solo per i test d Kendall e Spearman: calcolo del p esatto. Le opzioni sono TRUE / FALSE. Il default è NULL |
| conf.level | livello di confidenza |
| continuity | usato nei test d Kendall e Spearman: correzione di continuità. Le opzioni sono TRUE / FALSE. Il default è FALSE |
Script di esempio
E' possibile scaricare ed eseguire lo script dell'esempio: