Indice
Anova a una via (One Way Anova)
L’analisi della varianza (ANOVA) viene applicata, nell'esempio che segue, per analizzare la relazione fra una variabile categoriale (dataset: ChickWeight; alimentazione, Diet) e una variabile numerica di risposta (peso dei pulcini, weigth). Questo tipo di Analisi della varianza si chiama Anova a una via.
Equivale ad un test delle medie (Test t) su più di due gruppi, e ad una analisi di regressione lineare.
Vedi le voci: Anova con R; Contrasti
Test
I pacchetti
# per il piping e i grafici library(tidyverse) # per i risultati dei modelli in tabella library(broom)
Questi pacchetti non sono strettamente necessari.
I dati
| Diet | weight |
|---|---|
| 1 | 102,65 |
| 2 | 122,62 |
| 3 | 142,95 |
| 4 | 135,26 |
Il boxplot è un grafico utile per rappresentare i dati dell'Anova:
ChickWeight %>% ggplot(aes(Diet, weight)) + geom_boxplot(fill = "lightyellow", varwidth = T) + # proporzionale alla variabilità stat_summary(fun.data = mean_cl_boot, # punto che indica le medie geom = "point", size = 2, col = "blue")+ theme(legend.position = "null") + theme_minimal() # tema
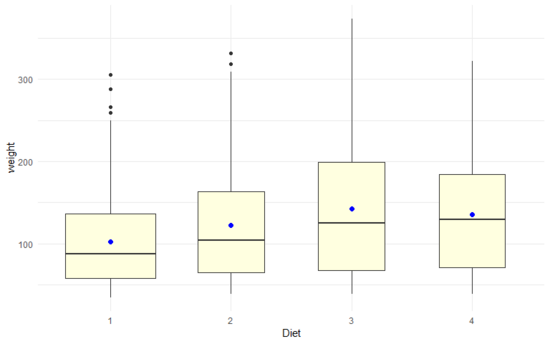
(possiamo notare che in realtà la distribuzione della variabile fra i casi non sarebbe adatta all'Anova)
Anova tra casi
Tabella dell'Anova
Ottieniamo la tabella Anova con il comando:
summary(aov.res)
## Df Sum Sq Mean Sq F value Pr(>F) ## Diet 3 155863 51954 10.81 6.43e-07 *** ## Residuals 574 2758693 4806 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
La devianza totale è pari alla somma dei valori nella colonna Sum Sq (155863 + 2758693). Possiamo verificarlo come segue:
# devianza totale y = ChickWeight$weight n = sum(!is.na(y)) # ricavo il valore dalla varianza var(y)*(n - 1)
## [1] 2914556
La dipendenza in media: eta quadro
La devianza spiegata dalla variabile indipendente è pari a 155862,7. Il rapporto fra devianza spiegata e devianza totale rappresenta la dipendenza in media, ovvero il valore $\eta^2$:
$$\eta^2 = \frac {\text{devianza spiegata}}{\text{devianza totale}}$$
Quindi:
155862.7 / (155862.7 + 2758693.3)
## [1] 0.05347734
L'indice $\eta^2$ ha una immediata corrispondenza con il coefficiente di determinazione $R^2$: la variabile Diet spiega il 5% della varianza del fenomeno in oggetto.
Vedi anche la funzione per calcolare direttamente l'eta quadro.
I contrasti
Il test F indica che le differenze di peso osservate nei gruppi definiti dalla variabile Diet sono statisticamente significative. Per valutare quale dieta è associata ad un maggior accrescimento, dobbiamo confrontare i gruppi, utilizzando i contrasti
Automatici
La procedura prevede la definizione di contrasti in automatico, che possono essere visualizzati nell'output del modello lineare (con `coef()`):
# summary.lm coef(aov.res)
## (Intercept) Diet2 Diet3 Diet4 ## 102.64545 19.97121 40.30455 32.61726
I coefficienti del modello indicano la media del primo gruppo (Diet1, Intercetta), assunto come riferimento, e le differenze fra i gruppi (Diet2 = media del gruppo 2 $-$ media del gruppo di riferimento. In pratica, e come si vede anche dal boxplot in Fig. 1, la dieta 1 ha la media più bassa, la 3 e la 4 le medie più alte.
Gli effetti delle diverse diete possono essere visualizzati come scomposizione della varianza (con summary() e split):
# summary.aov + split summary.aov(aov.res, split=list(Diet=list("2" = 1, "3" = 2, "4" = 3))) # e' preferibile specificare, per chiarezza dell'output, il nome della modalita # (ad es.: "2" = 1)
## Df Sum Sq Mean Sq F value Pr(>F) ## Diet 3 155863 51954 10.81 6.43e-07 *** ## Diet: 2 1 97 97 0.02 0.887 ## Diet: 3 1 74055 74055 15.41 9.71e-05 *** ## Diet: 4 1 81711 81711 17.00 4.29e-05 *** ## Residuals 574 2758693 4806 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Le differenze osservate fra alimentazioni sono statisticamente significative solo per le diete 3 e 4, e non per la dieta 3.
Solitamente, nei disegni sperimentali, il gruppo scelto come base è il gruppo di controllo.
Impostare i contrasti
Per impostare il contrasto con la dieta 4, useremo la funzione contr.treatment() (ad esempio), e impostiamo come base dei contrasti la quarta modalità contr.treatment(4, base = 4) (Vedi: I contrasti):
# cambio la base contrasts(ChickWeight$Diet) <- contr.treatment(4, base = 4)
Ripetiamo l'Anova e guardiamo il risultato di summary.lm():
aov(data = ChickWeight, weight ~ Diet) %>% summary.lm()
oppure (vedi piping (%>%))
summary.lm(aov(data = ChickWeight, weight ~ Diet))
## Call: ## aov(formula = weight ~ Diet, data = ChickWeight) ## ## Residuals: ## Min 1Q Median 3Q Max ## -103.95 -53.65 -13.64 40.38 230.05 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 135.263 6.382 21.195 < 2e-16 *** ## Diet1 -32.617 7.910 -4.123 4.29e-05 *** ## Diet2 -12.646 8.988 -1.407 0.160 ## Diet3 7.687 8.988 0.855 0.393 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 69.33 on 574 degrees of freedom ## Multiple R-squared: 0.05348, Adjusted R-squared: 0.04853 ## F-statistic: 10.81 on 3 and 574 DF, p-value: 6.433e-07
Guardiamo anche il risultato di summary() e split():
# componenti della varianza aov(data = ChickWeight, weight ~ Diet) %>% summary.aov(split=list(Diet=list("1" = 1, "2" = 2, "3" = 3)))
## Df Sum Sq Mean Sq F value Pr(>F) ## Diet 3 155863 51954 10.810 6.43e-07 *** ## Diet: 1 1 130570 130570 27.168 2.61e-07 *** ## Diet: 2 1 21777 21777 4.531 0.0337 * ## Diet: 3 1 3516 3516 0.732 0.3927 ## Residuals 574 2758693 4806 ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Anova entro casi, o con osservazioni ripetute (repeated measures)
In questo caso, è evidente che le misurazioni sono state ripetuto nel corso del tempo e su un certo numero controllato di pulcini. Utilizziamo quindi la procedura per l'Anova entro casi, ovvero inserendo come fonte di errore, sempre con la [[r:concetti_di_base:formula|formula]], le variabili che rappresentano le misurazioni ripetute, in questo caso: + Error(Chick/Time):
aovr.res <- aov(data = ChickWeight, weight ~ Diet + Error(Chick/Time)) aovr.res
## Call: ## aov(formula = weight ~ Diet + Error(Chick/Time), data = ChickWeight) ## ## Grand Mean: 121.8183 ## ## Stratum 1: Chick ## ## Terms: ## Diet Residuals ## Sum of Squares 155862.7 374242.8 ## Deg. of Freedom 3 46 ## ## Residual standard error: 90.19819 ## Estimated effects may be unbalanced ## ## Stratum 2: Chick:Time ## ## Terms: ## Residuals ## Sum of Squares 2306278 ## Deg. of Freedom 50 ## ## Residual standard error: 214.7686 ## ## Stratum 3: Within ## ## Terms: ## Residuals ## Sum of Squares 78172.81 ## Deg. of Freedom 478 ## ## Residual standard error: 12.78833
Il risultato scompone la varianza nei diversi strati; il test F è "depurato" dalla variabilità derivante da Chick/Time.
Il comando tidy() del pacchetto broom consente di avere un risultato semplificato e facilmente leggibile della tabella dell'Anova relativa:
aovr.res %>% tidy()
| stratum | term | df | sumsq | meansq | statistic | p.value |
|---|---|---|---|---|---|---|
| Chick | Diet | 3 | 155.862,66 | 51.954,2192 | 6,385945 | 0,0010399 |
| Chick | Residuals | 46 | 374.242,81 | 8.135,7134 | – | – |
| Chick:Time | Residuals | 50 | 2.306.277,64 | 46.125,5528 | – | – |
| Within | Residuals | 478 | 78.172,81 | 163,5414 | – | – |
Script di esempio
E' possibile scaricare ed eseguire lo script dell'esempio:
- Es-oneway-anova.R
# per il piping e i grafici library(tidyverse) # per i risultati dei modelli in tabella library(broom) # boxplot ChickWeight %>% ggplot(aes(Diet, weight)) + geom_boxplot(fill = "lightyellow", varwidth = T) + # proporzionale alla variabilità stat_summary(fun.data = mean_cl_boot, # punto che indica le medie geom = "point", size = 2, col = "blue")+ theme(legend.position = "null") + theme_minimal() # tema # anova tra casi aov.res <- aov(data = ChickWeight, weight ~ Diet) summary(aov.res) # per vedere i contrasti summary.lm(aov.res) summary.aov(aov.res, split=list(Diet=list("2" = 1, "3" = 2, "4" = 3))) # anova entro casi aovr.res <- aov(data = ChickWeight, weight ~ Diet + Error(Chick/Time)) aovr.res summary(aovr.res) # con broom tidy(aovr.res)
