Indice

Matrici testuali come grafi

Matrici testuali come grafi

Le matrici testuali possono essere analizzate ricorrendo alle misure e agli strumenti della network analysis (ampiezza, grado, centralità, densità, distanze, grappoli ecc.), in quanto una matrice delle co-occorrenze può essere direttamente trasformata in un grafo e rappresentata come network (matrice di adiacenza):

i termini rappresentano i nodi (da, a), e
i valori delle celle rappresenta il numero di link (o archi, o edges) fra i due nodi (ed eventualmente il peso).

Altre strutture di dati di uso comune nell'analisi testuale sono i dataframe dei link fra termini a due a due (edgelist), anch'essi direttamente interpretabili come grafi.

Testi e dati degli esempi, dove necessario anonimizzati, sono disponibili qui (file: es_twitter.rda). Gli script che seguono presuppongono che testi e dati siano in una sottocartella “dati” del progetto.

Con Quanteda

La funzione textplot_network() di uno dei pacchetti di Quanteda (quanteda.textplots) costruisce automaticamente il network a partire da una matrice testuale (termini documenti o delle cooccoorenze):

Vedi Quanteda

Le matrici testuali

# pacchetti
library(tidyverse)
library(quanteda)
quanteda_options(language_stemmer ="italian") 
library(quanteda.textplots)
 
# dati
load("dati/es_twitter.rda")

Costruiamo con Quanteda una matrice delle cooccorrenze (fcm: features cooccorrence matrix) degli hashtag, a partire da un dataset di messaggi di Twitter:

 
rt.fcm <- rt2 %>% 
  mutate(text = str_replace_all(text, "[\'’]", "' ")) %>% 
  corpus() %>% 
  # tokenizzazione
  tokens(remove_punct = T) %>% 
  # matrice documenti termini
  dfm() %>% 
  # selezione dei soli hashtags
  dfm_select("#*") %>% 
  # soglia di occorrenze
  dfm_trim(min_termfreq = 4) %>%  
  # matrice delle cooccorrenze
  fcm()

Consideriamo i primi dieci termini della matrice:

rt.fcm[1:10,1:10]

Feature co-occurrence matrix of: 10 by 10 features.
                        features
features                 #greenpass #greenpassday #greenpassrendeliberi ...
  #greenpass                      4           303                    52 ...
  #greenpassday                   0            10                   205 ...
  #greenpassrendeliberi           0             0                     2 ...
  #greenpassobbligatorio          0             0                     0 ...
  #portichiusi                    0             0                     0 ...
  #portualiditrieste              0             0                     0 ...
  #lilianasegre                   0             0                     0 ...
  #nogreenpass                    0             0                     0 ...
  #libertà                        0             0                     0 ...
  #portualitrieste                0             0                     0 ...

I termini costituiscono sia le righe che le colonne della matrice (nello stesso ordine). I valori delle celle rappresentano le co-occorrenze, ovvero il numero delle volte in cui due termini sono compresenti nello stesso messaggio.

I termini saranno i nodi del network, mentre le cooccorrenze verranno rappresentate dalle linee che collegano i nodi.

textplot_network

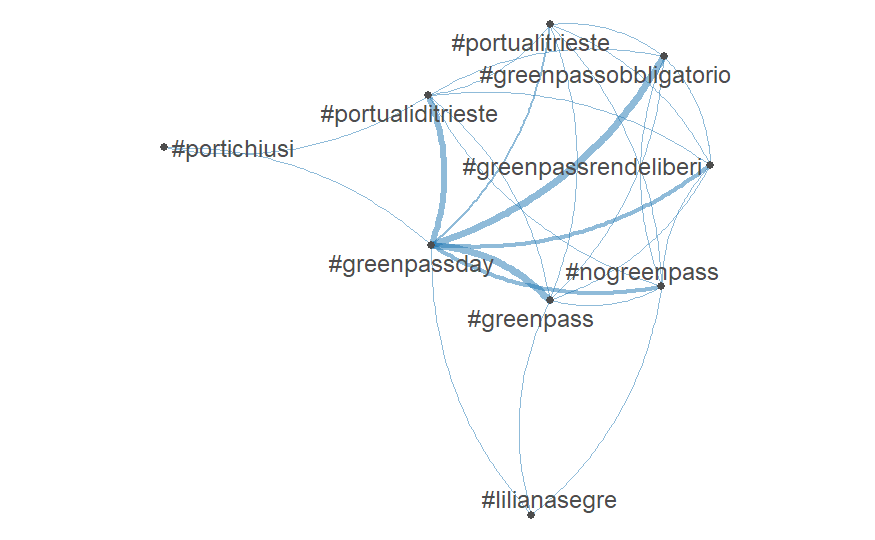
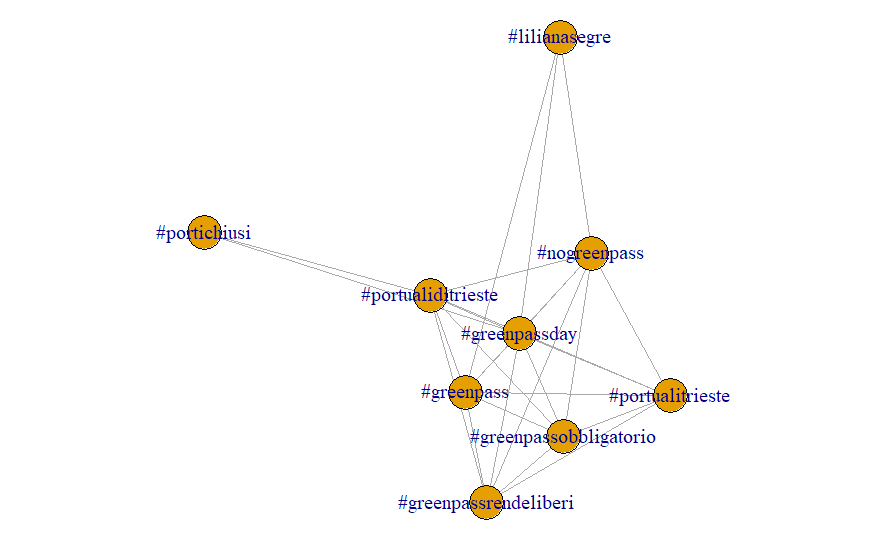
Applichiamo ora la funzione textplot_network(), che produrrà anche il grafico dei termini. Due termini (o categorie, nel caso dei network semantici) che co-occorrono in uno stesso testo sono legati come due nodi di una rete. Lo spessore dei link (edges) fra i nodi (vertices) è proporzionale al valore delle celle.

set.seed(345)
textplot_network(rt.fcm[1:10,1:10]) +
  coord_equal()

Note:

la funzione usa la sintassi di ggplot

set.seed() viene inserito per ottenere sempre la stessa rappresentazione grafica, in quanto la dispozione dei nodi nello spazio è casuale;

coord_equal(): quando si rappresentano i network è spesso preferibile usare un sistema di coordinate uguali (rapporto 1:1), per ridurre la distorsione (visiva) delle distanze fra i nodi

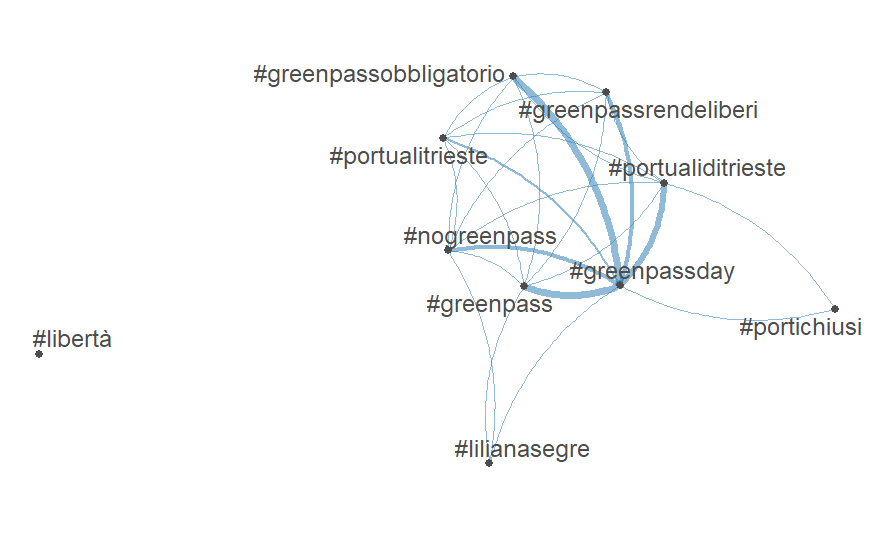
I nodi sono 9, anziché 10, perché la funzione elimina i nodi “isolati”, con frequenza inferiore a una soglia data.

set.seed(345)
textplot_network(rt.fcm[1:10,1:10], 
                 omit_isolated = F) +
  coord_equal()

as.igraph

In alternativa, è possibile – con la funzione as.igraph() di Quanteda (quanteda.textplots) – trasformare la matrice in un grafo di igraph, per esportarlo in un formato standard, e lavorarci con altre librerie o software.

g <- as.igraph(rt.fcm[1:10,1:10], 
               weighted = T)
g

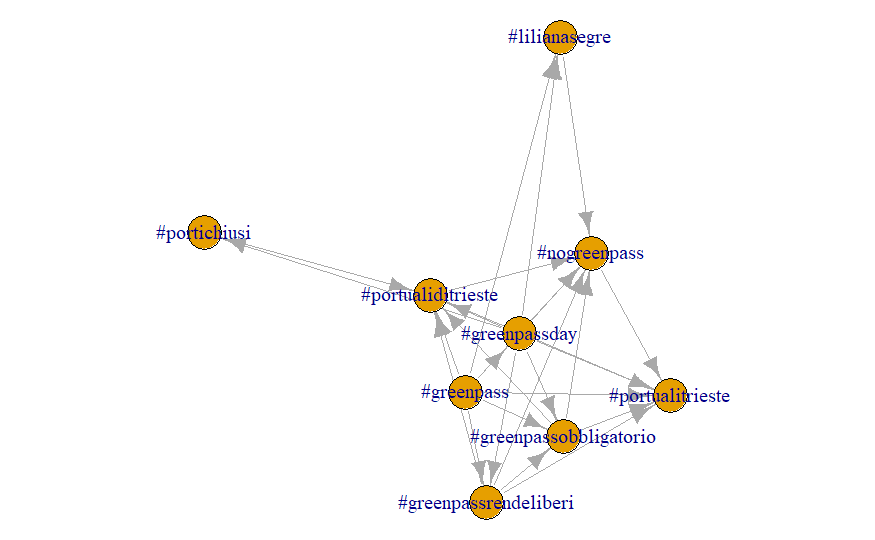
IGRAPH 6832679 DNW- 9 26 -- 
+ attr: name (v/c), frequency (v/n), weight (e/n)
+ edges from 6832679 (vertex names):
 [1] #greenpass            ->#greenpassday         
 [2] #greenpass            ->#greenpassrendeliberi 
 [3] #greenpassday         ->#greenpassrendeliberi 
 [4] #greenpass            ->#greenpassobbligatorio
 [5] #greenpassday         ->#greenpassobbligatorio
 [6] #greenpassrendeliberi ->#greenpassobbligatorio
 [7] #greenpassday         ->#portichiusi          
 [8] #greenpass            ->#portualiditrieste    
+ ... omitted several edges

Che potrà essere poi stampato con plot():

# margini
par(mar=c(0,0,0,0))
 
set.seed(345)
plot(g,
     asp = 1)

asp = 1 equivale a coord_equal() (rapporto 1:1)

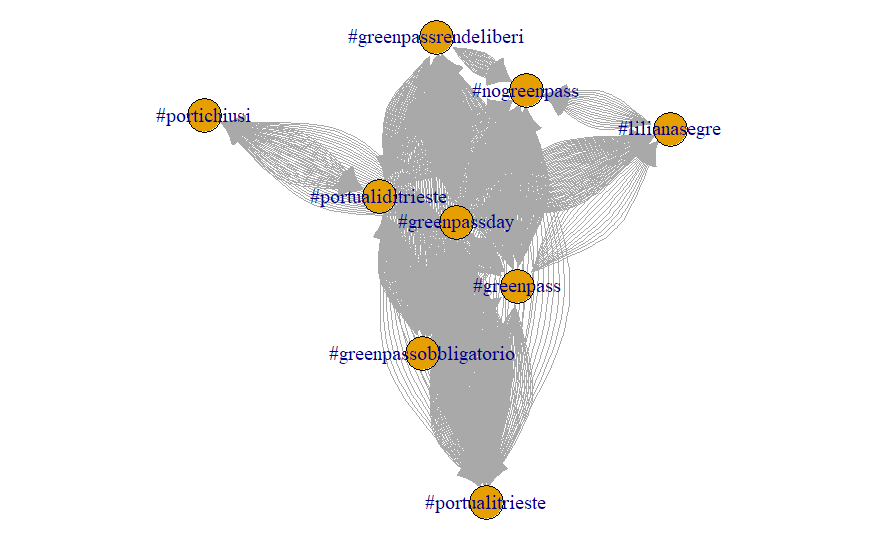
l'argomento weighted = T serve a far interpretare i valori nelle celle della matrice come pesi. Altrimenti, il grafo conterrebbe tanti links fra due nodi, quante sono le cooccorrenze, dando luogo ad una rappresentazione come quella che segue:

Script di esempio

text_network_quanteda.R

# pacchetti
library(tidyverse)
library(quanteda)
quanteda_options(language_stemmer ="italian") 
library(quanteda.textplots)
 
# dati
load("dati/es_twitter.rda")
 
# matrice delle co-occorrenze
rt.fcm <- rt2 %>% 
  mutate(text = str_replace_all(text, "[\'’]", "' ")) %>% 
  corpus() %>% 
  # tokenizzazione
  tokens(remove_punct = T) %>% 
  # matrice documenti termini
  dfm() %>% 
  # selezione dei soli hashtags
  dfm_select("#*") %>% 
  # soglia di occorrenze
  dfm_trim(min_termfreq = 4) %>%  
  # matrice delle cooccorrenze
  fcm()
 
# network
set.seed(345)
textplot_network(rt.fcm[1:10,1:10]) +
  coord_equal()
 
# grafo igraph
g <- as.igraph(rt.fcm[1:10,1:10], 
               weighted = T)

Con igraph

Grafo non orientato

Il network precedente, diversamente dal primo, è orientato, ovvero presenta - ad esempio - una freccia che va da #portichiusi a #portualitrieste e una che va in senso inverso.

Se stiamo lavorando con le semplici cooccorrenze di termini, preferiremo con tutta probabilità un grafo non orientato (diverso sarà invece il caso dei network concettuali o semantici).

Per operare questa trasformazione (ed altre) sul grafo, possiamo usare le funzioni del pacchetto igraph.

library(igraph)
 
# trasformo il grafo in un grafo non orientato
g <- g %>% 
  as.undirected()
g

IGRAPH d340f6b UNW- 9 26 -- 
+ attr: name (v/c), frequency (v/n), weight (e/n)
+ edges from d340f6b (vertex names):
 [1] #greenpass            --#greenpassday         
 [2] #greenpass            --#greenpassrendeliberi 
 [3] #greenpassday         --#greenpassrendeliberi 
 [4] #greenpass            --#greenpassobbligatorio
 [5] #greenpassday         --#greenpassobbligatorio
 [6] #greenpassrendeliberi --#greenpassobbligatorio
 [7] #greenpassday         --#portichiusi          
 [8] #greenpass            --#portualiditrieste    
+ ... omitted several edges

par(mar=c(0,0,0,0))
set.seed(345)
plot(g,
     asp = 1)

Attributi dei nodi e dei link

Il grafo contiene 9 nodi, 26 link, ed una serie di attributi relativi ai nodi e ai link, ereditati dalla matrice di partenza, così come il nome (che in plot() viene interpretato come etichetta dei nodi). Gli attributi dei nodi sono accessibili mediante le funzioni V(g) (per i nodi) e E(g) (per i link).

V(g)$name

[1] "#greenpass"             "#greenpassday"          "#greenpassrendeliberi" 
[4] "#greenpassobbligatorio" "#portichiusi"           "#portualiditrieste"    
[7] "#lilianasegre"          "#nogreenpass"           "#portualitrieste"

o le frequenze dei termini:

# frequenze dei termini
V(g)$frequency

[1]  302 1678  205  301   31  275   51  187  126

# pesi (co-occorrenze)
E(g)$weight

 [1] 303  52 205  82 303  58  31  47 278  43  64  19  16  51  41 187  26  31
[19]  39  16  28 126  16  37  21  24

La possibilità di aggiungere e modificare le proprietà di nodi e link è di fondamentale importanza per l'analisi di queste reti.

Da una matrice di adiacenza (cooccorrenze)

Un grafo può essere costruito dalla matrice delle cooccorrenze anche con la funzione graph_from_adjacency_matrix() di igraph¹⁾. Torniamo all'esempio precedente:

graph_from_adjacency_matrix(rt.fcm[1:10,1:10])

IGRAPH b9aaf63 DN-- 10 2248 -- 
+ attr: name (v/c)
+ edges from b9aaf63 (vertex names):
 [1] #greenpass->#greenpass    #greenpass->#greenpass   
 [3] #greenpass->#greenpass    #greenpass->#greenpass   
 [5] #greenpass->#greenpassday #greenpass->#greenpassday
 [7] #greenpass->#greenpassday #greenpass->#greenpassday
 [9] #greenpass->#greenpassday #greenpass->#greenpassday
[11] #greenpass->#greenpassday #greenpass->#greenpassday
[13] #greenpass->#greenpassday #greenpass->#greenpassday
[15] #greenpass->#greenpassday #greenpass->#greenpassday
+ ... omitted several edges

Volendo un grafo non orientato, ponderato e semplificato:

g2 <- graph_from_adjacency_matrix(rt.fcm[1:10,1:10],
                                  # pesi
                                  weighted = T) %>% 
  # non orientato
  as.undirected() %>% 
  # semplificato
  simplify() 
g2

IGRAPH 0776c35 UNW- 10 42 -- 
+ attr: name (v/c), weight (e/n)
+ edges from 0776c35 (vertex names):
 [1] #greenpass   --#greenpassday         
 [2] #greenpass   --#greenpassrendeliberi 
 [3] #greenpass   --#greenpassobbligatorio
 [4] #greenpass   --#portichiusi          
 [5] #greenpass   --#portualiditrieste    
 [6] #greenpass   --#lilianasegre         
 [7] #greenpass   --#nogreenpass          
 [8] #greenpass   --#libertà              
+ ... omitted several edges

Possiamo recuperare le informazioni sulle frequenze dei termini dai metadati della matrice, ed aggiungerle come attributo dei nodi:

V(g2)$frequency <- meta(rt.fcm, "margin", "object")[1:10]

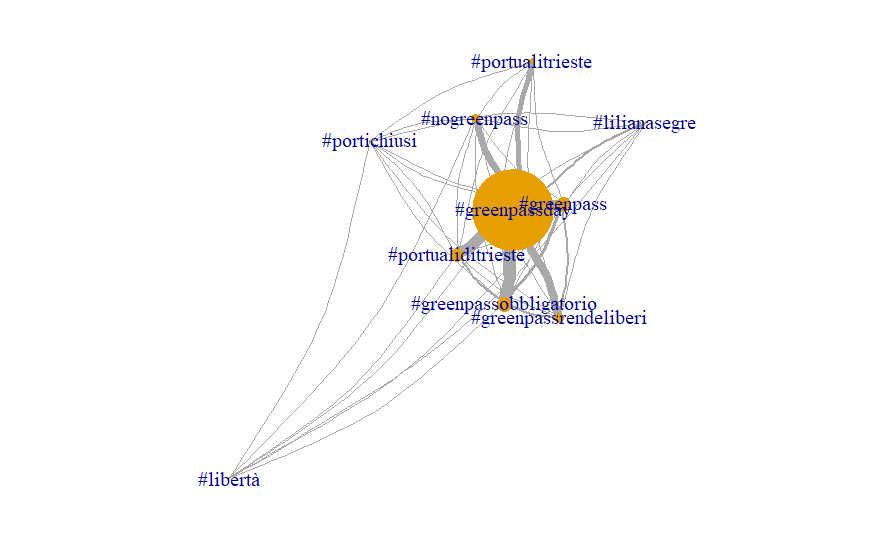
Nel grafico che segue, vediamo un esempio di uso degli attributi per modificare l'output:

set.seed(123)
par(mar = c(0,0,0,0))
plot(g2,
     edge.curved = 0.2,
     asp = 1,
     vertex.frame.color = "transparent",
     # dimensione dei nodi proporzionali alle frequenze
     vertex.size = V(g2)$frequency/max(V(g2)$frequency)*40,
     # spessore dei link proporzionali ai pesi
     edge.width = E(g2)$weight/max(E(g2)$weight)*10
     )

Grafo da un dataframe

Una lista di link (edgelist) si presenta in questo modo:

# trasformiamo la matrice dell'esempio precedente
df <- tidytext::tidy(rt.fcm[1:10,1:10]) %>% 
  rename(term1 = document,
         term2 = term,
         weight = count)
df

# A tibble: 52 × 3
   term1                  term2                  weight
   <chr>                  <chr>                   <dbl>
 1 #greenpass             #greenpass                  4
 2 #greenpass             #greenpassday             303
 3 #greenpassday          #greenpassday              10
 4 #greenpass             #greenpassrendeliberi      52
 5 #greenpassday          #greenpassrendeliberi     205
 6 #greenpassrendeliberi  #greenpassrendeliberi       2
 7 #greenpass             #greenpassobbligatorio     82
 8 #greenpassday          #greenpassobbligatorio    303
 9 #greenpassrendeliberi  #greenpassobbligatorio     58
10 #greenpassobbligatorio #greenpassobbligatorio      2
# … with 42 more rows

Il primo termine viene considerato come il nodo da cui parte il link, il secondo termine come quello di arrivo.

Importante è anche che la colonna con i valori delle co-occorrenze si chiami “weight”, affinché venga interpretato come sistema di pesi dalla funzione graph_from_data_frame(), e il grafo risulti ponderato.

graph_from_data_frame(df, 
                      # non orientato
                      directed = F) %>% 
  # semplificato
  simplify()
</code
 
<code rsplus>
IGRAPH f0bcd60 UNW- 10 42 -- 
+ attr: name (v/c), weight (e/n)
+ edges from f0bcd60 (vertex names):
 [1] #greenpass   --#greenpassday          #greenpass   --#greenpassrendeliberi 
 [3] #greenpass   --#greenpassobbligatorio #greenpass   --#portichiusi          
 [5] #greenpass   --#portualiditrieste     #greenpass   --#lilianasegre         
 [7] #greenpass   --#nogreenpass           #greenpass   --#libertà              
 [9] #greenpass   --#portualitrieste       #greenpassday--#greenpassrendeliberi 
[11] #greenpassday--#greenpassobbligatorio #greenpassday--#portichiusi          
[13] #greenpassday--#portualiditrieste     #greenpassday--#lilianasegre         
[15] #greenpassday--#nogreenpass           #greenpassday--#libertà              
+ ... omitted several edges

In questo caso, vogliamo un grafo non orientato, quindi specifichiamo l'argomento directed = F, e semplifichiamo.

Script di esempio

text_network_igraph.R

# pacchetti
library(tidyverse)
library(quanteda)
library(igraph)
 
# dati
load("dati/es_twitter.rda")
 
# matrice delle co-occorrenze
rt.fcm <- rt2 %>% 
  mutate(text = str_replace_all(text, "[\'’]", "' ")) %>% 
  corpus() %>% 
  # tokenizzazione
  tokens(remove_punct = T) %>% 
  # matrice documenti termini
  dfm() %>% 
  # selezione dei soli hashtags
  dfm_select("#*") %>% 
  # soglia di occorrenze
  dfm_trim(min_termfreq = 4) %>%  
  # matrice delle cooccorrenze
  fcm()
 
# dalla matrice di adiacenza
g2 <- graph_from_adjacency_matrix(rt.fcm[1:10,1:10],
                                  # pesi
                                  weighted = T) %>% 
  # non orientato
  as.undirected() %>% 
  # semplificato
  simplify() 
 
V(g2)$frequency <- meta(rt.fcm, "margin", "object")[1:10]
 
set.seed(123)
par(mar = c(0,0,0,0))
plot(g2,
     edge.curved = 0.2,
     asp = 1,
     vertex.frame.color = "transparent",
     # dimensione dei nodi proporzionali alle frequenze
     vertex.size = V(g2)$frequency/max(V(g2)$frequency)*40,
     # spessore dei link proporzionali ai pesi
     edge.width = E(g2)$weight/max(E(g2)$weight)*10
     )
 
# dal dataframe dell'edgelist
# trasformiamo la matrice dell'esempio precedente
df <- tidytext::tidy(rt.fcm[1:10,1:10]) %>% 
  rename(term1 = document,
         term2 = term,
         weight = count)
 
graph_from_data_frame(df, 
                      # non orientato
                      directed = F) %>% 
  # semplificato
  simplify()

Analisi testuale, Text Network Analysis, Text Mining

¹⁾

Quanteda prevede la costruzione di matrici di co-occorrenze (features cooccurrence matrix, fcm()). Se si usa tm, la matrice documenti-termini andrà trasformata “a mano” in una matrice termini-termini.